Fotogrammetrie speelt een cruciale rol in het vastleggen en verwerken van ruimtelijke informatie. De technologie stelt ons in staat om op basis van foto’s en beeldmateriaal uiterst nauwkeurige 3D-modellen en coördinaten te berekenen. Dit wordt mogelijk gemaakt door wiskundige modellen en berekeningen. In dit artikel besteden we aandacht aan het cameramodel dat gebruikt wordt in de fotogrammetrie. Dat is het wiskundige model waarmee de werking van de camera wordt beschreven.
Fotografie en de camera obscura
Bij fotogrammetrie wordt de omgeving vastgelegd op fotobeelden door middel van een camera. Dit kunnen reguliere camera’s zijn, of special ontwikkelde camera’s. Zolang de toegepaste camera voldoet aan enkele basiseisen, maakt de keuze voor de toegepaste camera echter geen verschil voor de principes en berekeningen. Hierin ligt een deel van de charme van fotogrammetrie, het kan zowel met dure specialistische apparatuur, als met goedkope “off-the-shelf” componenten.
Begrip van de fotogrammetrische berekeningen vereist eerst een analyse van de werking van de camera. De camera in zijn meest eenvoudige vorm is de camera obscura, of wel de donkere kamer. Dit is een compleet verduisterde kamer met één kleine opening in één van de wanden, zoals getoond in Figuur 1. De omgeving buiten de donkere kamer is verlicht door natuurlijke of kunstmatige lichtbronnen. Het licht weerkaatst op de omgeving buiten en enkele lichtstralen zullen precies in de richting van het kleine gat in de donkere kamer reflecteren. Daarmee komt de straal op de achterwand van de kamer uit. Zodoende ontstaat een afbeelding op de achterwand.
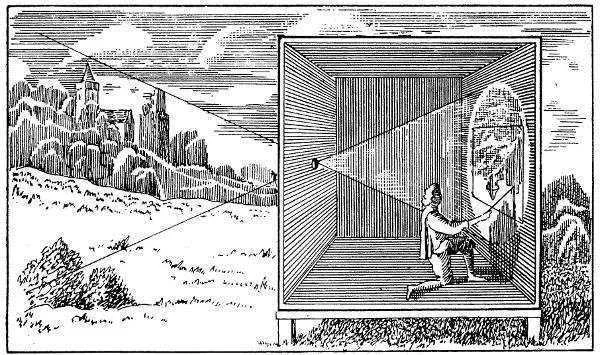
Figuur 1 - Camera Obscura (Athanasius Kircher, Ars Magna Lucis Et Umbrae, 1645)
De camera obscura kent in de praktijk enkele nadelen. Voor een scherpe afbeelding moet het gat in de wand zo klein mogelijk zijn. Bij een groter gat zullen er lichtstralen uit diverse richtingen op dezelfde plek uitkomen. Dat levert een onscherpe afbeelding op. Een klein gat betekent echter ook dat er minder licht in de ruimte valt, waardoor de afbeelding niet voldoende helder wordt. Dit wordt opgelost door toepassing van een objectief. Dat is een samenstelling van lenzen waarmee de opening in de wand vergroot wordt, terwijl het wel mogelijk blijft een scherpe afbeelding te verkrijgen. Vanuit fotogrammetrisch perspectief is het nadeel van een camera met een objectief dat deze op een bepaalde afstand scherp gesteld moet worden. De artistieke fotograaf heeft dit effect, dat scherpte-diepte wordt genoemd, juist als kunstvorm omarmd.
Iedere moderne fotocamera grijpt terug op het principe van de donkere kamer. Het gat is echter vervangen door een objectief en de achterwand door een lichtgevoelige sensor, zoals een CCD of CMOS chip. De grootte van de donkere kamer kan erg klein zijn. Denk aan een camera die in een mobiele telefoon moet worden geplaatst. De afstand van gat tot achterwand bedraagt dan hooguit een paar millimeter. Analoge fotogrammetrische camera’s voor luchtopnamen hadden doorgaans een erg grote ruimte, waarbij de afstand van gat tot wand ongeveer 30 centimeter bedroeg.
De camera obscura kunnen we formaliseren als in het schema van Figuur 2. Het model wordt dan het pinhole cameramodel genoemd. In het Nederlands wordt dit ook wel vertaald als de gaatjescamera of speldenprikcamera, maar toepassing van die begrippen zal in de praktijk eerder tot verwarring dan begrip leiden, dus spreken wij hier van de pinhole camera.
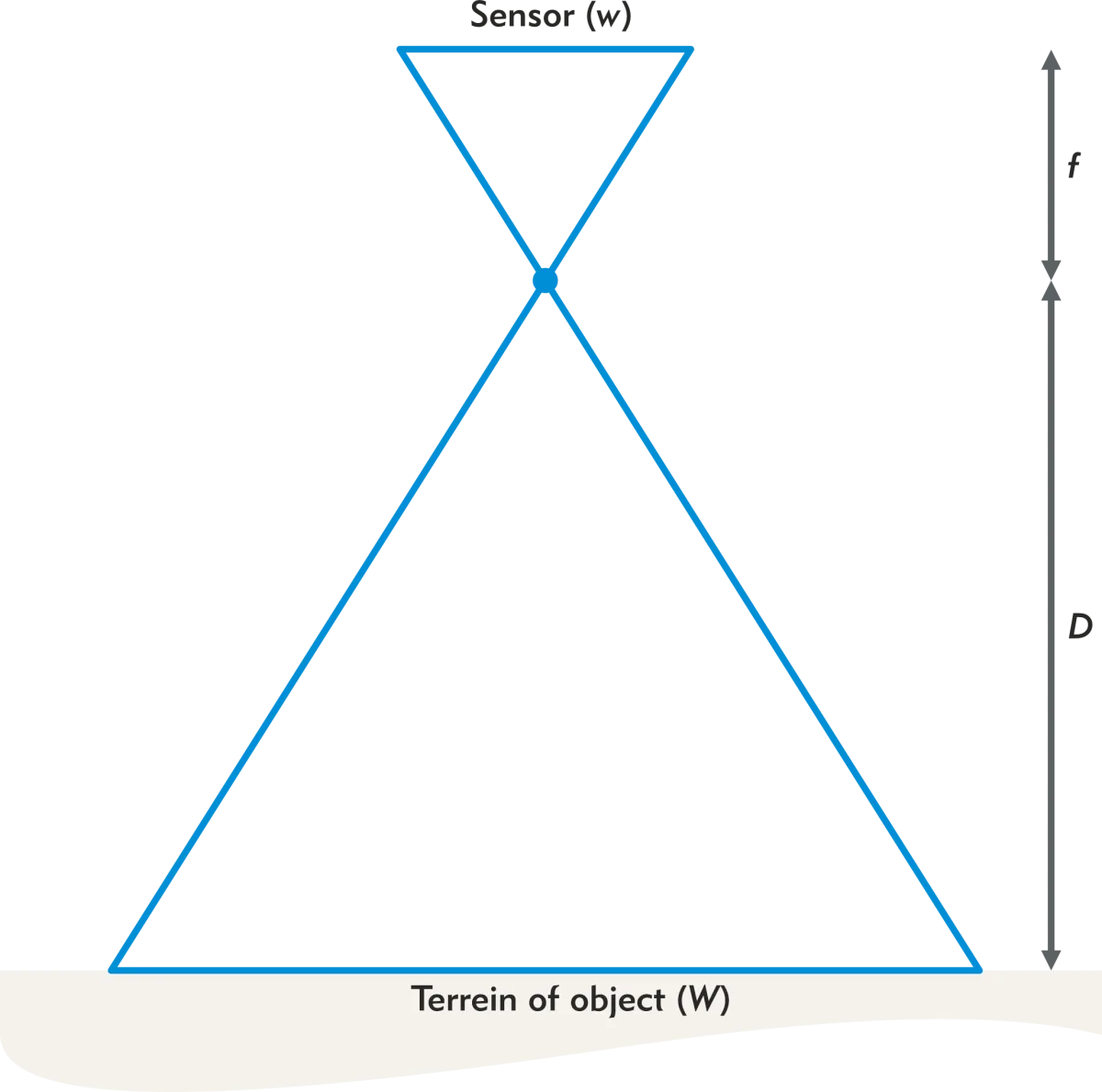
Figuur 2 - Schematische weergave van de pinhole camera
De pinhole (ofwel het speldengat) waar het licht doorkomt noemen we formeel het optisch centrum. De achterwand bevat de lichtgevoelige sensor. In het tijdperk van analoge fotografie met filmrolletjes werd dat ook wel de gevoelige plaat genoemd. De breedte van de sensor drukken we uit met de letter 𝑤. De afmetingen van de sensor moeten door de fabrikant opgegeven worden. Digitale spiegelreflexcamera’s voor de consumentenmarkt hebben bijvoorbeeld vaak een breedte van 24 mm (het zogeheten APS-C).
De afstand van de sensor tot de lensopening wordt de brandpuntsafstand of cameraconstante genoemd. Deze afstand wordt aangeduid met de letter 𝑓 of de letter 𝑐. De afstand tot het object wordt aangeduid met de letter 𝐷 voor close-range fotogrammetrie, of bij luchtfotografie met de letter 𝐻.
In de afbeelding van de camera obscura is te zien dat de wereld “op zijn kop” afgebeeld wordt. Dit geldt ook in het pinhole cameramodel. Iedere afbeelding is gespiegeld over de x-as en de y-as van de sensor. Dit komt overeen met een draaiing van 180 graden. Fabrikanten van camera’s realiseren zich dat de meeste gebruikers de voorkeur geven aan een afbeelding die niet op zijn kop staat. De inwendige software corrigeert daarom direct voor deze spiegeling (met soms nog aanvullende bewerkingen, zoals een spiegeling over de verticale as voor het effectief maken van selfies). Deze gecorrigeerde afbeelding is wat we uiteindelijk bekijken in ons fotoalbum, op Instagram of in fotogrammetrische uitwerkingssoftware.
De afbeelding op de sensor noemen we het negatiefvlak. De gecorrigeerde afbeelding noemen we het positiefvlak. Figuur 3 toont het positiefvlak als een virtuele lijn in het pinhole cameramodel. Het punt 𝑃 wordt afgebeeld als 𝑝′ op het negatiefvlak en als 𝑝 op het positiefvlak.
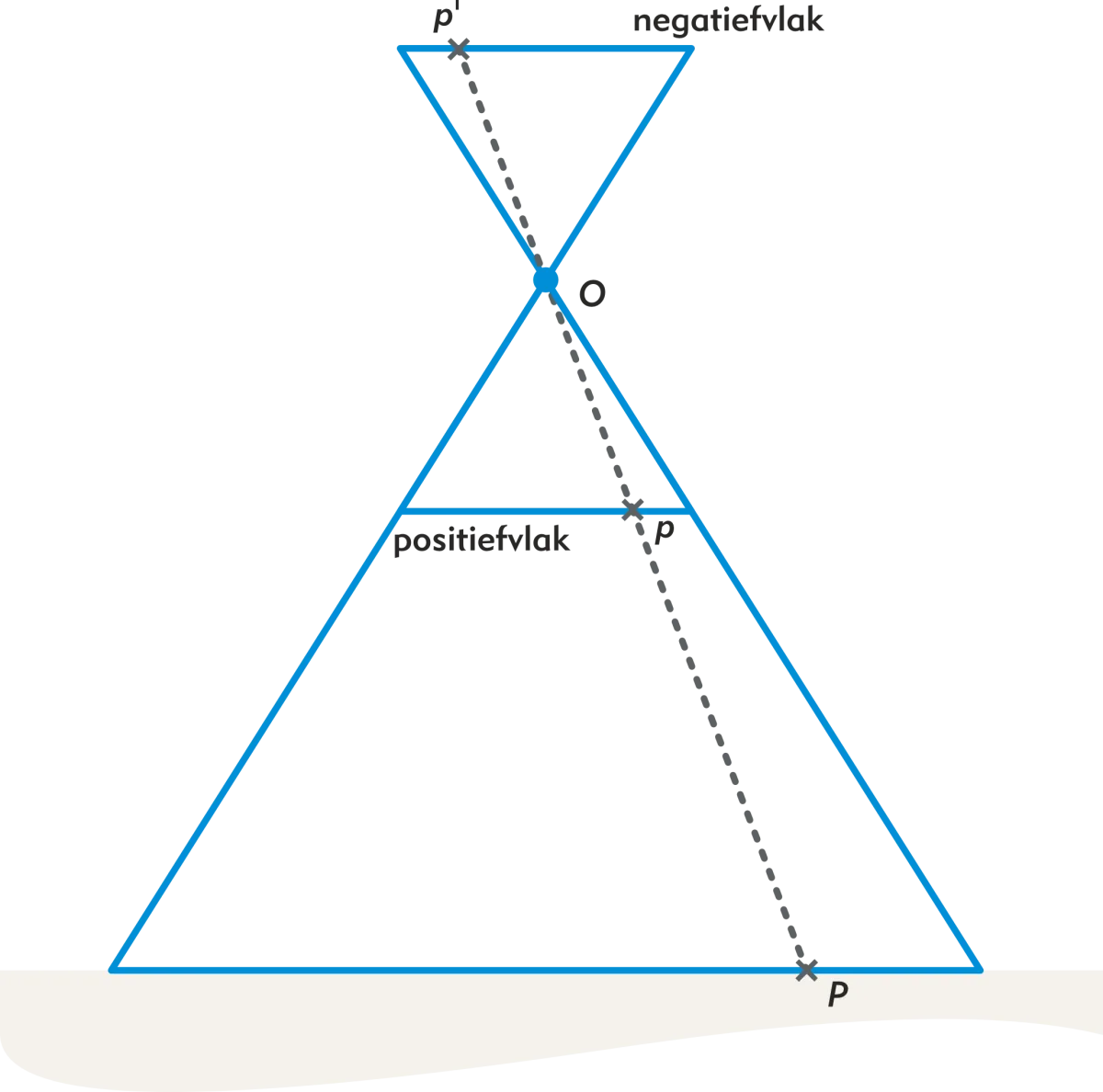
Figuur 3 - Negatiefvlak en Positiefvlak
De centrale projectie
De pinhole camera kan wiskundig beschreven worden als een centrale projectie. De centrale projectie is een projectieve transformatie waarbij een N-dimensionale ruimte wordt afgebeeld op een (N-1)-dimensionale deelruimte. In het geval van fotogrammetrie beelden we de driedimensionale ruimte dus af op een tweedimensionale foto. De centrale projectie is een projectieve transformatie waarbij sprake is van een projectiecentrum. Voor ieder punt in het terrein kan een lijn worden getrokken naar de afbeelding van dat punt op de foto. In de centrale projectie snijden al deze lijnen elkaar in het projectiecentrum. Bij een ideale camera valt het projectiecentrum samen met het optisch centrum.
Nu is gebleken dat we de fotografie kunnen modelleren als een centrale projectie, is het mogelijk om iedere foto te beschouwen als een coördinaattransformatie van terreinstelsel naar fotostelsel. Bij close range fotogrammetrie wordt in plaats van het terreinstelsel ook het begrip objectstelsel gebruikt. De transformatie is op hoog abstractieniveau als volgt te noteren:
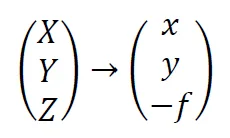
In dit artikel hanteren we de conventie dat terreincoördinaten in hoofdletters worden geschreven en de fotocoördinaten als kleine letters. Terreincoördinaten zijn doorgaans immers ook vrij groot, terwijl coördinaten en afstanden op de foto veel kleiner zijn. Doorgaans wordt in de software ook de conventie gehanteerd dat terreincoördinaten in meters worden opgeslagen en fotocoördinaten in millimeters.
Bovenstaande transformatie toont ook direct dat er sprake is van een projectie. Iedere coördinaat krijgt dezelfde z-coördinaat, namelijk −𝑓, ofwel de brandpuntsafstand. We raken dus een dimensie kwijt. De transformatie van terreinstelsel naar fotostelsel bestaat uit een rotatie, translatie en verschaling. Dus kunnen we deze schrijven als:
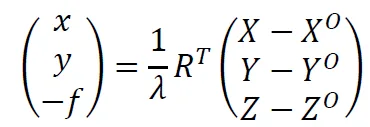
Hierin is 𝜆 de schaalfactor, 𝑅 de rotatiematrix en zijn 𝑋𝑂, 𝑌𝑂 en 𝑍𝑂 de locatie van het projectiecentrum in het terreinstelsel. De rotatiematrix kan gedefinieerd worden als rotatie van terreinstelsel naar fotostelsel, maar ook als rotatie van fotostelsel naar terreinstelsel. Helaas bestaat hiervoor in het vakgebied geen conventie en blijft dit bij ieder project een potentiële bron van fouten en frustratie.
Collineariteit en collineariteitsvergelijkingen
In het pinhole cameramodel is gebleken dat lichtstralen uit het terrein via een rechte lijn door het optisch centrum op de sensor terecht komen. Uit de centrale projectie blijkt dat dit geldt voor ieder punt dat afgebeeld wordt. Dit leidt tot een belangrijke constatering die de basis vormt voor alle fotogrammetrische berekeningen:
Een punt 𝑃 in het terrein ligt altijd op één lijn met het projectiecentrum 𝑂, de afbeelding op het positiefvlak 𝑝 en de afbeelding op het negatiefvlak 𝑝’.
Deze eigenschap wordt collineariteit genoemd. Uiteraard geldt dit alleen onder de aanname dat lichtstralen ook daadwerkelijk een rechte lijn volgen. Dat is niet altijd het geval. Refractie, lensvertekening en aardkromming zorgen ervoor dat de aanname van een rechte lijn niet altijd opgaat. Vooralsnog negeren we deze effecten en schakelen we een model in waarin iedere lichtstraal een perfecte rechte lijn volgt. Bij het uitschakelen van het model zullen we moeten beoordelen of deze aanname terecht was.
De collineariteit volgt uit de centrale projectie. De vergelijking van de centrale projectie kunnen we uitschrijven als drie onafhankelijke vergelijkingen:
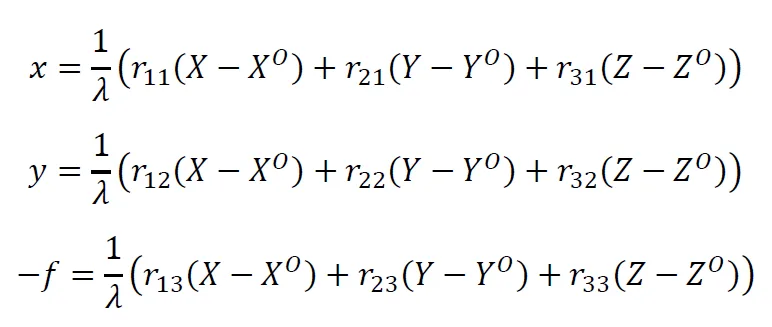
Hierin staat iedere 𝑟 voor de elementen van de rotatiematrix 𝑅. In de praktijk is de schaalfactor 𝜆 van een foto niet bekend. Door middel van substitueren kunnen de drie vergelijkingen echter herschreven worden tot twee onafhankelijke vergelijkingen zonder schaalfactor:
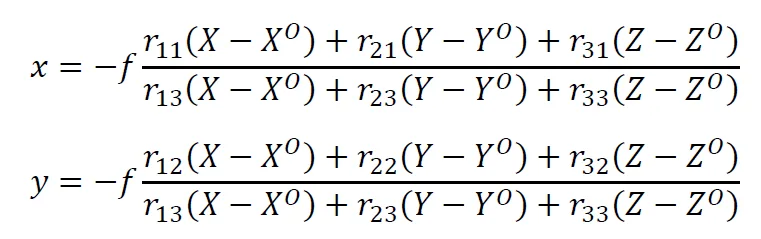
Merk op dat de schaalfactor nu in feite is vervangen door een factor die afhankelijk is van de brandpuntsafstand 𝑓. De hobbyfotograaf snapt intuïtief dat dit logisch is. Bij gebruik van een zoomlens vergroot hij bij het inzoomen de waarde van 𝑓 en komen de onderwerpen dichterbij. De schaal wordt dus groter. Bij het uitzoomen wordt de lens korter, dus wordt 𝑓 kleiner. Er is dan meer op de foto te zien, dus is de schaal kleiner.
De twee bovengenoemde vergelijkingen worden de collineariteitsvergelijkingen genoemd. Ze beschrijven de relatie tussen objecten in het terreinstelsel, de afbeelding ervan op het positiefvlak van de foto en de rotatie en translatie van de camera.
Van cameramodel naar coördinaatbepaling
Met de wiskundige modellering van de werking van de camera en het opstellen van de collineariteitsvergelijkingen, zijn de formules beschikbaar om uit foto's driedimensionale coördinaten te berekenen. In deel 2, het artikel Coördinaatbepaling is beschreven hoe dat werkt.



