Fotogrammetrie speelt een cruciale rol in het vastleggen en verwerken van ruimtelijke informatie. De technologie stelt ons in staat om op basis van foto’s en beeldmateriaal uiterst nauwkeurige 3D-modellen en coördinaten te berekenen. Dit vereist dat de gebruikte camera gekalibreerd is. In dit artikel wordt beschreven hoe een camerakalibratie werkt.
In het artikel over het cameramodel is beschreven op welke wijze een camera wiskundig gemodelleerd wordt. Met deze modellering kunnen vervolgens coördinaten berekend worden met behulp van een triangulatie en bundelblokvereffening. Dit artikel beschrijft hoe de elementen uit de wiskundige modellering van de camera bepaald kunnen worden met behulp van een camerakalibratie.
Brandpuntsafstand
In de waarnemingsvergelijkingen treffen we parameters aan voor de terreincoördinaten van de verbindingspunten en voor de uitwendige oriëntering van de foto. Al deze parameters worden opgenomen als onbekende parameters in de vereffening. In de waarnemingsvergelijking treffen we echter ook 𝑓, de brandpuntsafstand aan.
Bij veel projecten in de luchtfotogrammetrie hoeven we ons over deze waarde geen zorgen te maken. De fabrikant van de camera levert jaarlijks een kalibratierapport waarin de juiste waarde voor 𝑓 is opgenomen. Bij close-range toepassingen, of bij toepassing van een drone, kennen we de brandpuntsafstand doorgaans niet. Deze moet bepaald worden door middel van een kalibratie.
Vanuit het perspectief van een bundelblokvereffening is het kalibreren van een brandpuntsafstand gelukkig overzichtelijk. We kunnen 𝑓 eenvoudig opvoeren als onbekende parameter en een waarde voor de brandpuntsafstand schatten in de vereffening. Dit brengt wel aanvullende eisen aan de opname met zich mee, omdat de kans op een singuliere matrix in dit geval groter is. In het geval van drone- en luchtfotogrammetrie zijn de brandpuntsafstand en de vlieghoogte bijvoorbeeld sterk met elkaar gecorreleerd. Dit is te verhelpen door in één vereffening opnames op te nemen van twee verschillende vlieghoogtes.
Hoofdpuntsverschuiving
Vanuit de centrale projectie volgt dat de oorsprong van het fotostelsel ligt in het projectiecentrum. Het midden van een foto kent derhalve de coördinaten (0,0,−𝑓). Zo werd dat ook gedefinieerd in het pinhole cameramodel in het artikel over het cameramodel. De realiteit is echter dat het midden van de sensor zelden exact onder het projectiecentrum ligt. Door onnauwkeurigheden tijden de fabricage van de camera of het objectief, ligt de sensor meestal iets verschoven.
Een lichtstraal die loodrecht op het sensorvlak invalt, heeft op dat moment coördinaten die iets naast het midden van het sensorvlak ligt. Dit punt, gedefinieerd door de lijn die loodrecht op het sensorvlak gaat en door het projectiecentrum loopt, heet het hoofdpunt. De afstand tussen het midden van de sensor en het hoofdpunt heet de hoofdpuntsverschuiving. Tot nu toe gingen alle vergelijkingen ervan uit dat de hoofdpuntsverschuiving gelijk was aan 0. Nu dit niet het geval blijkt te zijn, moeten de vergelijkingen hierop aangepast worden. De aangepaste collineariteitsvergelijkingen zijn:
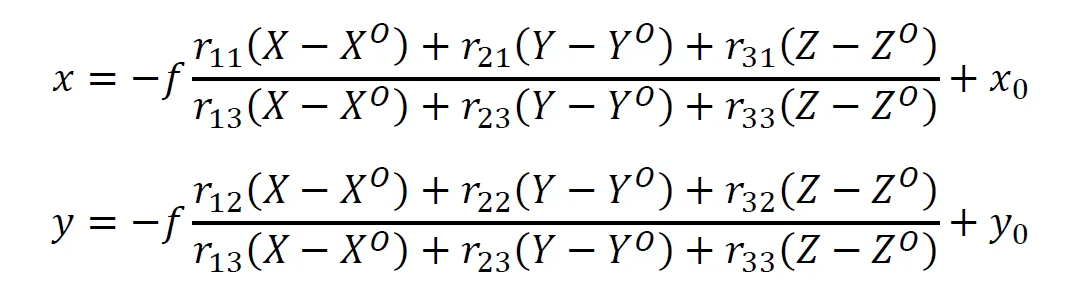
Hierin staan 𝑥0 en 𝑦0 voor de hoofdpuntsverschuiving (Figuur 1). Ook hier geldt dat de hoofdpuntsverschuiving terug te vinden is in het camerakalibratierapport van de leverancier van een fotogrammetrische camera. Voor close-range toepassingen moet de waarde bepaald worden door de hoofdpuntsverschuiving op te nemen als onbekende in de vereffening.
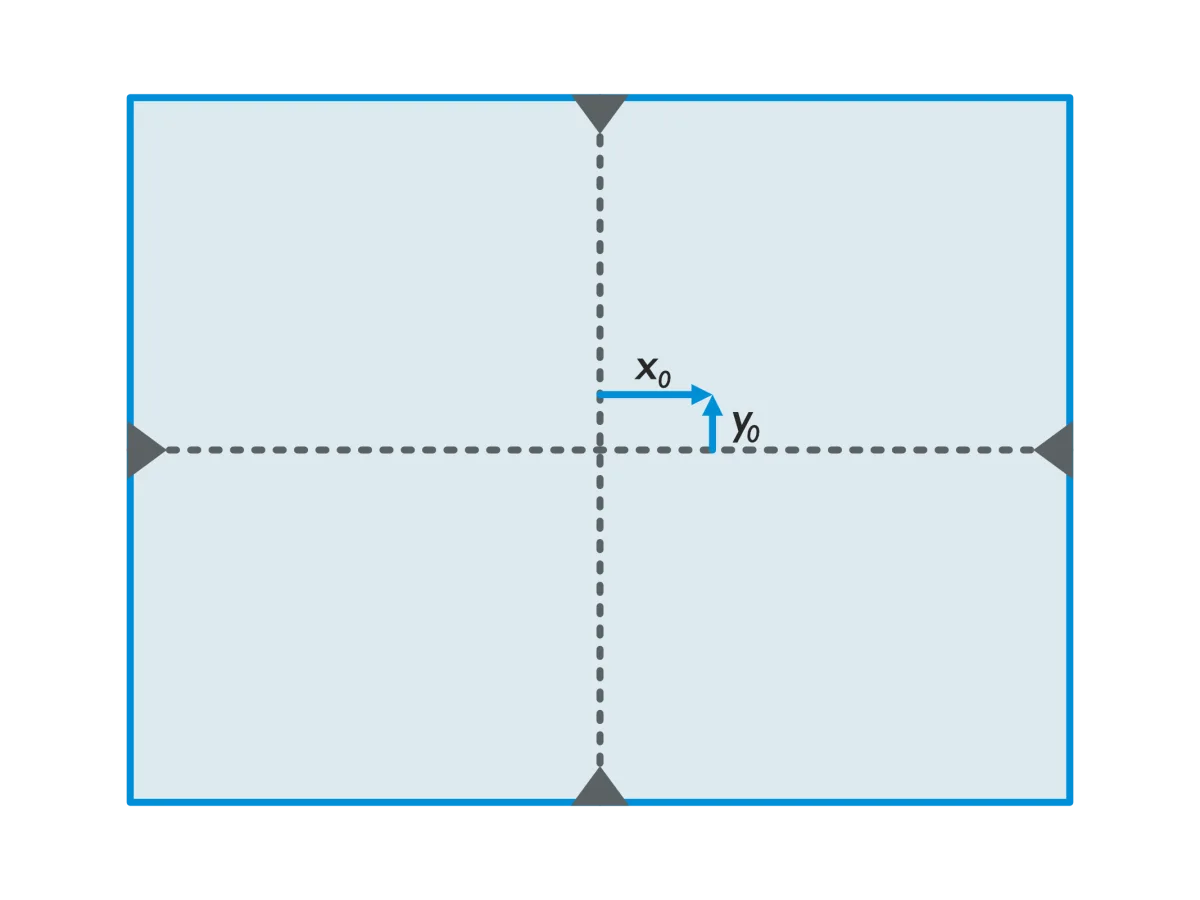
Figuur 1 - Hoofdpunt op een sensor
Lensvertekening
De aanname dat lichtstralen recht door het gaatje van de pinhole-camera lopen, gaat niet op doordat er in werkelijkheid een objectief is geplaatst. Zelfs bij objectieven van hoge kwaliteit zal er enige mate van vertekening zijn, waardoor de aanname dat lichtstralen rechtdoor gaan niet meer klopt. Daarom moet de lensvertekening bepaald worden.
De lensvertekening wordt opgesplitst in twee componenten: radiële lensvertekening en tangentiële lensvertekening. De radiële lensvertekening wordt beschreven met een polynoom. Voor iedere afstand vanaf het hoofdpunt geeft deze polynoom de toe te passen correctie. Doorgaans wordt voor de polynoom het lensvertekeningsmodel van Brown ingezet. Verder kunnen ook andere vormen van vertekening worden gemodelleerd, zoals decentering en scheefstand.
Additionele parameters
Uit de beschrijving van de hoofdpuntsverschuiving en lensvertekening blijkt dat het mogelijk is om diverse correcties op fotocoördinaten toe te passen. De grootte van deze correcties kan geschat worden in de bundelblokvereffening. Veel fotogrammetrische software kent de mogelijkheid voor additionele parameters. Dit zijn extra onbekenden die aan het functiemodel kunnen worden toegevoegd om daarmee andere afwijkingen van de standaard collineariteitsvergelijking te modelleren. Er zijn additionele parameters met (historisch) bestaansrecht. Zo kent veel software additionele parameters om een vertekening als gevolg van het scannen van analoge foto’s toe te passen. Enkele voorbeelden van additionele parameters die in vereffeningssoftware zijn terug te vinden:
- Vertekeningen als gevolg van scannen;
- Vertekeningen als gevolg van kromtrekken analoge foto;
- Affiene transformatie;
- Afstand tussen het GNSS/INS-systeem en het projectiecentrum van de camera (de lever arms);
- Rotatie tussen het GNSS/INS-systeem en fotostelsel (de misalignment);
- Correctie voor cycle slip per vliegstrook (een verkeerd opgeloste fasemeerduidigheid in de GNSS-berekening);
- Correctie voor rolling shutter effecten;
- Constante verschuiving van het projectiecentrum.
Additionele parameters mogen alleen aan een bundelblokvereffening worden toegevoegd als deze fysisch te onderbouwen zijn. De toepassing van de additionele parameters moet dus te verklaren zijn uit de omstandigheden tijdens de opname.
Laboratoriumkalibratie
Uit het voorgaande blijkt dat het mogelijk is om een camerakalibratie uit te voeren tijdens de opname. Toch zijn de beste resultaten te verwachten in een kalibratie in een gecontroleerde omgeving. Een zogeheten laboratoriumkalibratie. Geodelta heeft de voorzieningen het voor het uitvoeren van een laboratoriumkalibratie en kan ook ondersteunen bij het uitvoeren van kalibraties tijdens een speciale opnamevlucht.



